Hypothesis testing is a fundamental concept in statistical analysis that allows researchers to make inferences about populations based on sample data.
However, hypothesis testing is not immune to errors. Two common types of errors that can occur during hypothesis testing are Type I and Type II errors.
In this blog post, we will explore the differences between Type I and Type II errors, their implications, and how they can affect research outcomes.
Type I Error
Type I error, also known as a “false positive,” occurs when the null hypothesis is rejected when it is actually true. In other words, it is the incorrect rejection of a true null hypothesis.
The definition of type I error in statistics is an error that happens when sample results lead to the null hypothesis being rejected even though it is true. To put it simply, the error of accepting the alternative hypothesis when the results may be attributed to chance.
Also referred to as the alpha error, it causes the researcher to assume that there is a difference between two observations that are actually the same. The level of significance the researcher selects for his test corresponds to the possibility of type I error. Here, the likelihood of committing a type I error is referred to as the level of significance.
Assume that a company’s research team determined, based on data, that more than 50% of all customers like the new service the company launched, even though the actual percentage is less than 50%.
Type II Error
Type II error, also known as a “false negative,” occurs when the null hypothesis is not rejected when it is actually false. In other words, it is the failure to reject a false null hypothesis.
Type II errors occur when the null hypothesis is accepted based on data when it is actually untrue. It occurs when the researcher fails to deny the false null hypothesis. It is sometimes referred to as a beta error and is indicated by the Greek letter beta (β).
Type II errors occur when a researcher rejects an alternative hypothesis despite the fact that it is true. It validates a proposition, which ought to be refused. The researcher concludes that the two observations are identical when they are not.
The power of the test is similar to the likelihood of making such an error. The chance of rejecting the null hypothesis, which is incorrect and has to be rejected, is indicated by the term “power of test” in this context. As the sample size increases, so does the power of the test, which results in a lower likelihood of type II error.
For instance, let’s say that despite the fact that more than 50% of all customers appreciate the new service the company launched, the research team of the organization claims, based on sample results, that less than 50% of all customers do.
Example: Type I and Type II errors
If you decide to get tested for COVID-19 based on mild symptoms, there are two potential errors that could happen:
Type I error (false positive): the test results indicate that you have coronavirus when in fact you do not.
Type II error (false negative): the test results indicate that you do not have coronavirus when in fact you do.

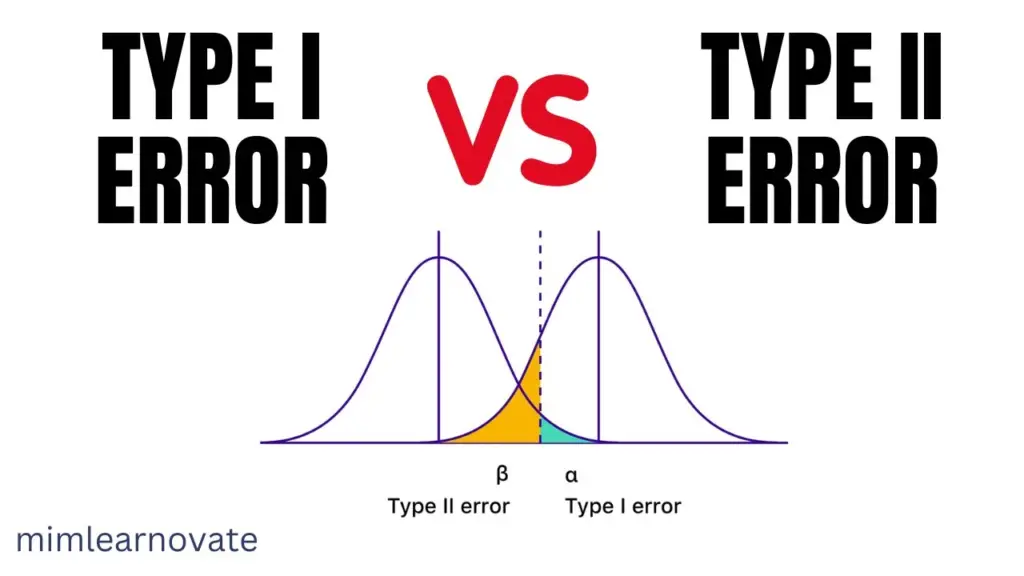
Type I vs Type II error
- Type I error occurs when the outcome is the rejection of a null hypothesis that is, in fact, true. Type II error happens when a false null hypothesis is accepted as the result of the sample.
- Type I error, often known as false positive, occur when a positive result is obtained despite the null hypothesis being rejected. Contrarily, Type II error, commonly referred to as false negatives or a negative outcome, results in the null hypothesis being accepted.
- Type I error occur when the null hypothesis is valid but is incorrectly rejected. Contrarily, a type II error mistake occurs when the null hypothesis is true but is incorrectly accepted.
- Type I error frequently assert something that is not actually there, resulting in a false hit. On the other hand, a type II error misses identifying something that is present.
- The sample as the level of significance determines the likelihood of making type I error. On the other hand, the chance of making a type II error is the same as the test’s power.
- Type I error is denoted by the Greek letter “α” Contrary to type II error, which is indicated by the Greek character “β”
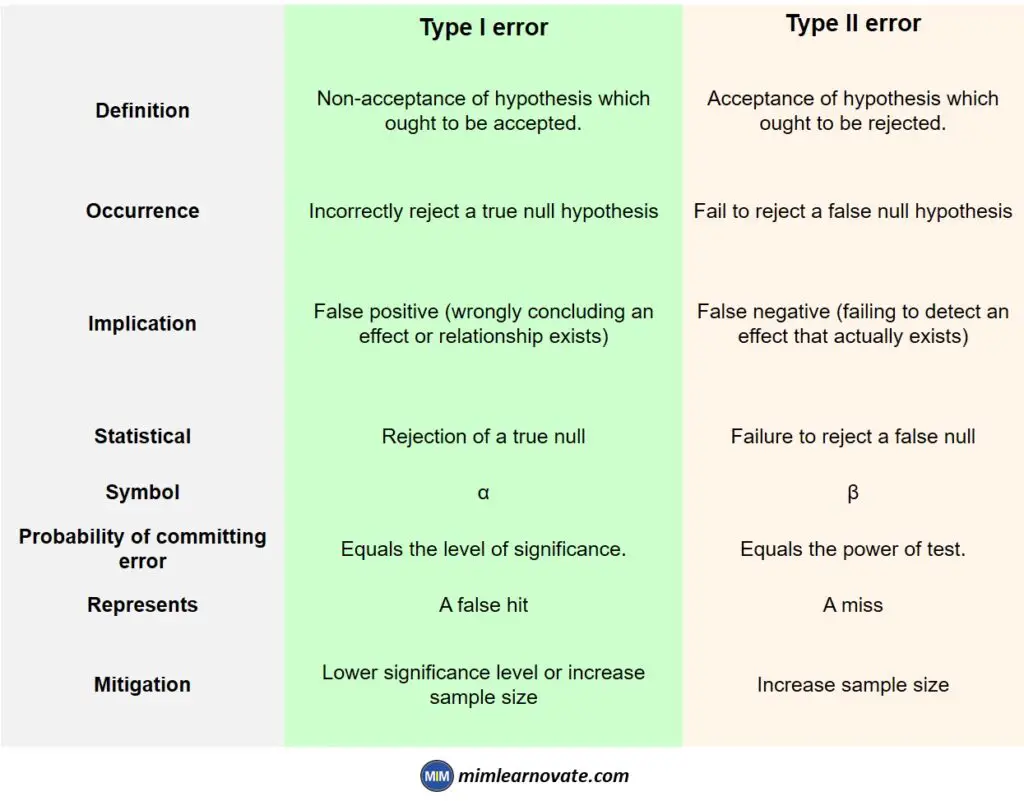
| Type I error | Type II error | |
| Definition | Non-acceptance of hypothesis which ought to be accepted. | Acceptance of hypothesis which ought to be rejected. |
| Occurrence | Incorrectly reject a true null hypothesis | Fail to reject a false null hypothesis |
| Implication | False positive (wrongly concluding an effect or relationship exists) | False negative (failing to detect an effect that actually exists) |
| Statistical | Rejection of a true null | Failure to reject a false null |
| Symbol | α | β |
| Probability of committing error | Equals the level of significance. | Equals the power of test. |
| Represents | A false hit | A miss |
| Mitigation | Lower significance level or increase sample size | Increase sample size |
Is a Type I or Type II error worse?
The severity of Type I and Type II errors depends on the context and the specific consequences associated with each error. In general, the relative importance of Type I and Type II errors can vary based on the nature of the study, the field of research, and the potential impact of the decision being made.
In some situations, Type I errors may be considered more serious. For example, in medical testing, a false positive (Type I error) could lead to unnecessary medical procedures, treatments, or psychological distress for patients. Similarly, in criminal justice, a Type I error could result in an innocent person being wrongly convicted.
On the other hand, in certain cases, Type II errors may have more significant consequences. For instance, in drug testing, a false negative (Type II error) could result in a potentially effective drug being rejected, denying patients access to a beneficial treatment. In quality control, a Type II error could allow defective products to enter the market, posing risks to consumers.
Ultimately, the severity of Type I and Type II errors should be evaluated on a case-by-case basis, considering the specific context, potential consequences, and the preferences of stakeholders involved. Researchers and decision-makers should carefully consider the potential impact of both types of errors and aim to strike an appropriate balance based on the specific objectives and constraints of their study or decision-making process.
Conclusion:
Type I and Type II errors are integral parts of hypothesis testing, and understanding their differences is essential for interpreting research findings accurately.
Type I errors involve rejecting a true null hypothesis, leading to false positives, while Type II errors involve failing to reject a false null hypothesis, leading to false negatives.
Researchers must strike a balance between these errors based on the importance of the research question, the desired level of confidence, and the available resources. By considering these factors, researchers can conduct hypothesis testing with greater accuracy and make informed decisions based on statistical evidence.
Remember, hypothesis testing is a powerful tool, but it is not infallible. Awareness of Type I and Type II errors allows researchers to critically evaluate research outcomes and draw appropriate conclusions, ultimately enhancing the reliability and validity of statistical analyses.