Understanding Critical Values in Statistics: Definitions, Types, and Applications

Rate this post

The concept of critical value is frequently used in statistics. Making judgments regarding testing hypotheses, calculating confidence intervals for a population-based sample of data, and other statistical issues can be assisted by understanding the critical values.

The critical value acts as a reference point for data analysis in addition to hypothesis testing. It supports statisticians in generating reliable inferences from data and maintaining the validity of their findings.

In this article, we will explore the critical value with its definition, confidence interval, types, and applications.

Critical Values

The critical value in statistics is a starting point used when comparing to a test statistic in hypothesis testing. It helps in deciding whether to reject or accept the null hypothesis. The null hypothesis typically posits that there is no significant difference or suggestion between variables under study.

In contrast, the alternative hypothesis suggests the opposite, stating that there is a significant difference or relationship. The critical value, which may or may not be an integer, is determined based on the desired significance level of the test and the distribution of the test statistic.

The test statistic that defines the upper and lower bounds of a confidence interval or the threshold of statistical significance in a test is known as the critical value. It indicates how far that you must go from the distribution’s mean in order to cover a specific amount of the overall variation in the data (i.e., 90%, 95%, 99%).

Your critical value will be the same in all scenarios if you are building a 95% confidence interval and utilizing a p = 0.05 statistical significance threshold.

Confidence interval

It is possible to evaluate the beginning of confidence for a one-tailed or two-tailed test. Study that the condition for a hypothesis test demands a 95% confidence interval. This is how the critical significance can be found.

Step 1: The confidence level is subtracted from 100 percent. 100% – 95% = 5%.

Step 2: You must transform this quantity to decimals. Thus, α = 5%.

Step 3: If the evaluation is one-tailed, phase 2’s alpha level will be the identical amount. However, the alpha level will be reduced by 2 if the test has two possible outcomes.

Step 4: The critical value can be found from the associated distribution table using the alpha value, based on the kind of test that was performed.

Types of Critical Values

F-Critical Value

The study of variance & regression modeling depends heavily on the F-critical value. Such a value of significance determines whether to accept or reject the null hypothesis in a variance-based hypothesis test.

It is typically written as Fα, df1, df2, and where denotes the degree of significance and df1, and df2 denote the denominator’s and nominator’s respective degrees of freedom.

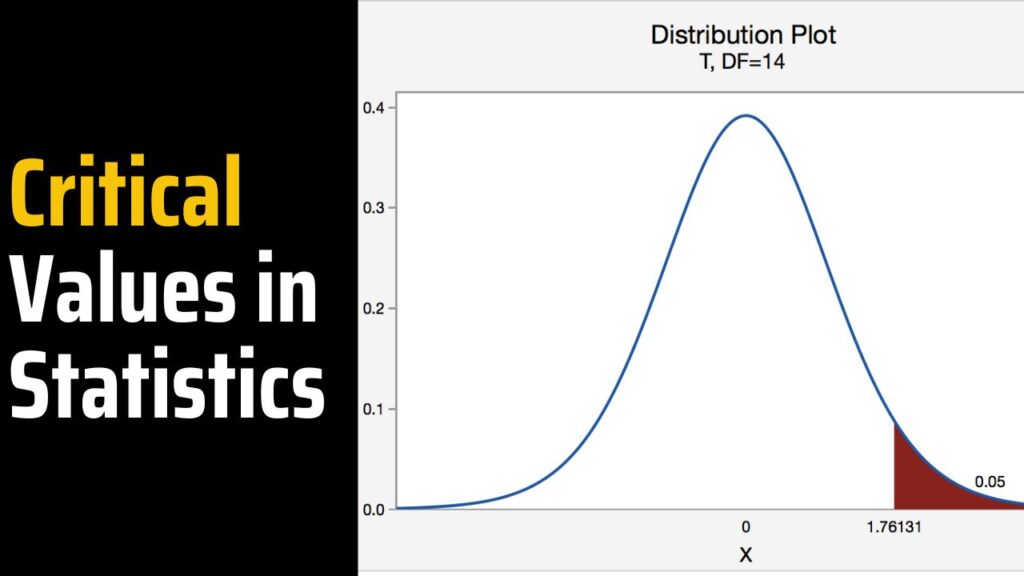
T-Critical Value

In testing for hypotheses for tiny samples where the population standard deviation is unidentified, the T-critical value is used. It aids in determining whether there is a notable difference between the sample mean and the population mean.

Z-Critical Value

When the sample size is significant and the data is distributed normally, the Z-critical value is used. For quantities and means, it is frequently utilized.

Chi-Square Critical Value

Both freedom testing & the fit quality analyses use the Chi-square critical value. It evaluates how category variables are related.

Example

In this section, we will explore the critical value with the help of examples.

Example 1:

Calculate the critical value Z Left tail test if 𝛼 = 0.012.

Solution:

Step 1: Find a confidence level

Subtract 𝛼 form 0.5, thus

Level of confidence = 0.5 – 0.012

Level of confidence = 0.488

Step 2: Using the Z table Find the table value

Z = 2.26

Step 3: Conclusion

Because the test is left tail the critical value becomes -2.26

Example 2:

With the sample size of 25 at a level of significance alpha = 0.025

Solution:

Step 1:

level of significance

n = 25

α =0.025

Step 2:

Degree of freedom

Df = k – 1, Df = 25 – 1

Df = 24

Step 3:

Then, we use one tail T distribution table at k = 24 and α = 0.025 is 2.0639

Step 4:

C = Critical value = 2.0639.

You can also utilize online tools to find critical values of t, z, f, and chi-square tests according to the distribution tables.

Daily life application

Drug Effectiveness

Let’s say a pharmaceutical business produces a brand-new medication with the promise of significantly lowering cholesterol. A sample of patients is chosen, and their blood cholesterol levels have been evaluated before and after taking the medication to test this.

It is possible to tell how a medicine has an effect that is statistically significant by contrasting the population’s mean to the critical value.

Election Polling

The possibility of error is affected by critical values. Voters’ opinions get recorded after selecting an appropriate collection of them. Analysts can determine the range in which genuine votes stand by computing the confidence interval using the critical value.

Final Words

In this article, we will explore the critical value with definitions, formulas, confidence intervals, types, and applications in detail. In addition, you can easily understand the critical value and related problems.

FAQs

1: What is intended by critical value?

The dimension of the test statistic that specifies the upper and lower bounds of a confidence interval or that creates the level of statistical implication in a statistical test is denoted as the vital rate.

2: How do critical value and p-value differ from one another?

Therefore, the crucial interval identifies the range across which our test statistic must fall to qualify for H₀ to be accepted. The p-value is somewhat the reverse in that it emphasizes the region outside of the crucial period. Suppose H₀ is correct, it predicts the likelihood that t or more severe values would develop.

3: What are the two critical values?

It is -1.645 for a lower-tailed test. However, if a two-tailed test is used, the critical values for the estimated degrees of freedom and the column that matches are -1.96 and 1.96, respectively.