Principal Components Analysis (PCA) using SPSS

Principal Component Analysis (PCA) serves the purpose of reducing a set of measured variables into a smaller number of independent linear combinations, known as principal components.

The goal is to retain as much of the original variables’ variability as possible.

In this article, we will demonstrate how to perform PCA using SPSS Statistics and guide you through the steps to interpret the results effectively. Also, we will discuss different assumptions your data must meet for PCA to produce valid results.

Principal Components Analysis (PCA)

Principal Component Analysis (PCA) is a statistical technique used to model the variation in a set of variables by representing them in terms of a smaller number of independent linear combinations, known as principal components.

It is a valuable technique for reducing the number of variables in a dataset, and it shares many similarities with exploratory factor analysis. The main objective of PCA is to transform a larger set of variables into a smaller set of ‘principal components,’ which are artificial variables representing the most significant variance in the original dataset.

The calculation of each principal component involves taking a linear combination of an eigenvector of the correlation matrix (or covariance matrix or sum of squares and cross-products matrix) with the variables. The corresponding eigenvalues represent the variance associated with each principal component, reflecting their importance in capturing the variability within the dataset.

Common Uses of PCA

1. Measurement of Variables: In scenarios where you have measured numerous variables, such as 7-8 questions/statements in a questionnaire, and suspect that some of these variables measure the same underlying construct (e.g., organizational learning), PCA can help identify highly correlated variables. You can include only the variables that best represent the construct in your measurement scale (e.g., questionnaire) and remove the rest.
2. Creating New Measurement Scales: When constructing a new measurement scale (e.g., questionnaire), uncertainty may arise about whether all the included variables effectively measure the desired construct (e.g., organizational learning). PCA allows you to test whether the construct ‘loads’ onto all or only some variables. This process helps determine if certain variables do not adequately represent the construct and should be eliminated from the new measurement scale.
3. Shortening Existing Measurement Scales: PCA is useful for testing whether an existing measurement scale (e.g., questionnaire) can be shortened by including fewer items (e.g., questions/statements). This is beneficial when redundant items exist, and a shorter questionnaire may lead to higher response rates.

It is important to note that although PCA and factor analysis are conceptually different, in practice, they are often used interchangeably, and PCA is included within the ‘Factor procedure‘ in SPSS Statistics.

SPSS Statistics: Understanding Assumptions for Principal Components Analysis (PCA)

When conducting Principal Components Analysis (PCA) in SPSS Statistics, it is crucial to ensure that your data meets specific assumptions for a valid and reliable analysis.

These assumptions help determine the suitability of using PCA for your dataset. Although checking these assumptions may require some additional tests and considerations, it is a necessary step in the analysis process.

It’s important to note that real-world data often differs from ideal textbook examples. Therefore, it’s not uncommon for one or more assumptions to be violated. However, even when such violations occur, there are potential solutions to address them.

To conduct a Principal Components Analysis (PCA), several assumptions need to be satisfied:

Assumption #1: PCA requires having multiple variables measured at the continuous level, although ordinal variables are also frequently used. Continuous variables are represented by ratio or interval data, such as revision time (in hours), intelligence (measured by IQ scores), exam performance (ranging from 0 to 100), weight (in kg), and more. Ordinal variables are commonly encountered in PCA, such as various Likert scales, ranging from ‘strongly agree’ to ‘strongly disagree,’ ‘never’ to ‘always,’ ‘not at all’ to ‘very much,’ or ‘not important’ to ‘extremely important.’

Assumption #2: PCA relies on Pearson correlation coefficients, which require a linear relationship between all variables. While this assumption is generally met, the use of ordinal data can somewhat relax it. To test for linearity, scatterplots can be employed, although considering over 500 linear relationships might be excessive. Randomly selecting a few possible relationships for testing can be sufficient. In case non-linear relationships are observed, transformations can be applied.

The items under analysis should exhibit normality and linearity, as correlations form the foundation for factor extraction in the analysis.

Items should be formulated in a way that allows for sufficiently high correlations, which are crucial for effective factor extraction.

Assumption #3: To obtain reliable PCA results, your data should have adequate sample sizes. Various rules-of-thumb have been proposed, often considering an absolute sample size or a multiple of the number of variables. Generally, a minimum of 150 cases or 5 to 10 cases per variable is recommended. An adequate sample size is essential to ensure that correlations between variables can converge into distinct and meaningful “factors.”

Here are few methods to detect sampling adequacy: 

• the Kaiser-Meyer-Olkin (KMO) Measure of Sampling Adequacy for the overall data set;
• KMO measure for each individual variable. 

Assumption #4: Suitable for Data Reduction For successful data reduction in PCA, adequate correlations between variables are essential. SPSS Statistics employs Bartlett’s test of sphericity to detect suitability.

Assumption #5: Outliers can significantly impact your results. SPSS Statistics suggests identifying outliers as component scores greater than 3 standard deviations from the mean.

Assumption #6: The content areas and items used in the analysis should be based on a well-defined theoretical or conceptual framework. This ensures that meaningful correlations can be identified and extracted.

Assumption #7: The sample should possess a certain level of homogeneity, enabling the measurement of the construct within its relevant context in the specific population.

Using SPSS Statistics, you can check assumptions #2, #3, #4, and #5 to ensure the validity of your PCA results. Accurate testing and interpretation of these assumptions are crucial for a meaningful analysis.

Example: Analyzing Employee Traits by Principal Components Analysis (PCA)

In this example, a company director seeks to hire a new employee who possesses specific qualities, including high motivation, dependability, enthusiasm, and commitment. To identify suitable candidates for interviews, the director devises a questionnaire comprising 25 questions that he believes will assess these desired traits. A total of 315 potential candidates participate in the questionnaire.

The questions in the questionnaire are thoughtfully designed to represent the four constructs of interest as follows:

1. Motivation: Questions Qu3, Qu4, Qu5, Qu6, Qu7, Qu8, Qu12, and Qu13 are associated with motivation.
2. Dependability: Questions Qu2, Qu14, Qu15, Qu16, Qu17, Qu18, and Qu19 are associated with dependability.
3. Enthusiasm: Questions Qu20, Qu21, Qu22, Qu23, Qu24, and Qu25 pertain to enthusiasm.
4. Commitment: Questions Qu1, Qu9, Qu10, and Qu11 are related to commitment.

The ultimate goal is to determine a comprehensive score for each candidate based on their responses. These scores will then be utilized to grade and evaluate the potential recruits.

To achieve this analysis, the company director employs SPSS Statistics, a powerful statistical software widely used for data analysis and interpretation. With SPSS Statistics, he can efficiently process the questionnaire responses and extract meaningful insights regarding each candidate’s suitability for the job.

By employing data-driven techniques like Principal Component Analysis (PCA) or Factor Analysis, the director can identify the most significant factors contributing to motivation, dependability, enthusiasm, and commitment. These analytical approaches enable him to combine multiple questionnaire items into composite scores for each construct, simplifying the evaluation process and facilitating informed decision-making.

How to perform Test for PCA in SPSS Statistics?

Performing Principal Component Analysis (PCA) in SPSS Statistics involves a series of 18 steps to analyze your data when none of the five assumptions mentioned in the previous section, “Assumptions,” have been violated.

These steps guide you through the process of conducting PCA and obtaining the initial results. At the end of these steps, we will also show you how to interpret the outcomes derived from PCA.

However, it is essential to note that the SPSS Statistics procedure for PCA is not always straightforward. Depending on the results of assumption tests conducted during the analysis and the initial components extracted, you may need to repeat some or all of the steps. In doing so, you might have to choose different options within the SPSS Statistics procedure or follow additional procedures to achieve the most accurate and meaningful outcomes.

Step-by-Step Guide for Principal Components Analysis (PCA) in SPSS Statistics

To begin the PCA process, click on “Analyze” from the main menu, then select “Dimension Reduction,” and finally, choose “Factor…” as depicted below:

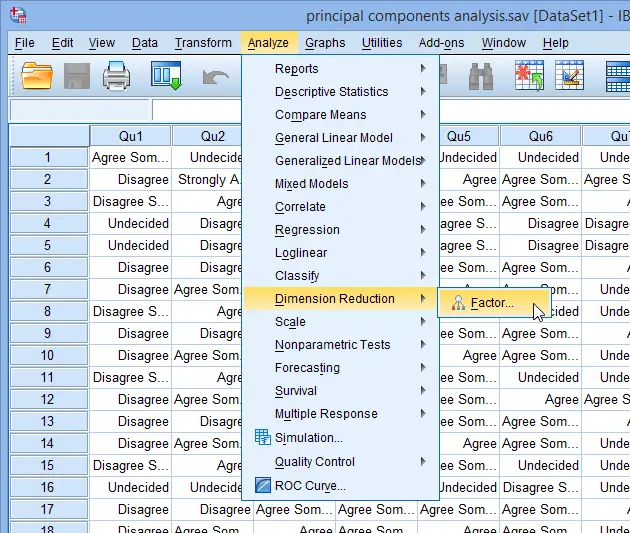
After the first step, the “Factor Analysis” dialogue box will appear, allowing you to proceed with the analysis. This dialogue box presents variables on the left side.

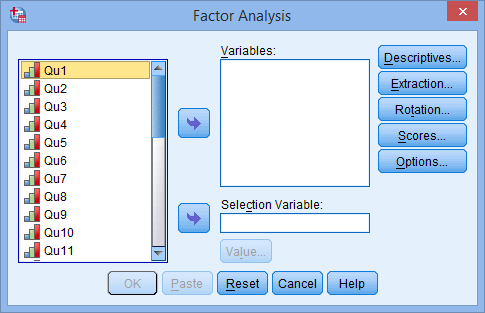
Transfer all the variables you wish to include in the analysis (in this example, Qu1 to Qu25) into the “Variables:” box by using the Right arrow button, as shown in the dialogue box.

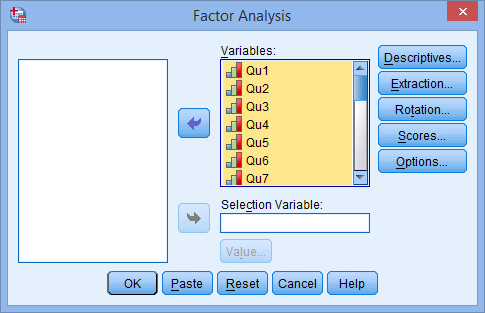
Click on the “Descriptives” button to open the “Factor Analysis: Descriptives” dialogue box, which allows you to specify additional options.

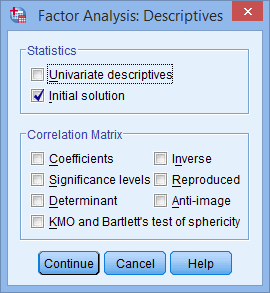
Here, you can check the options for Coefficients, KMO and Bartlett’s test of sphericity, Reproduced, and Anti-image from the “Correlation Matrix” area.

Click on “Continue” to return to the Factor Analysis dialogue box.

Click on the “Extraction” button to access the “Factor Analysis: Extraction” dialogue box.

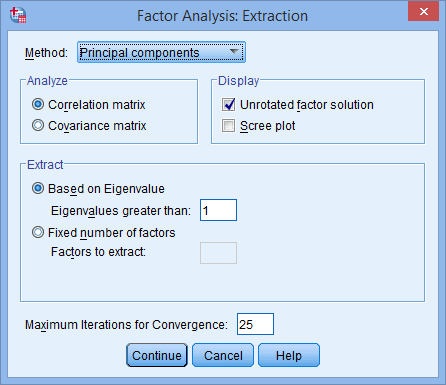
Keep all the defaults, but also select “Scree plot” in the “Display” area, which aids in visualization.

Click “Continue” to return to the Factor Analysis dialogue box.

Click on the “Rotation” button, leading you to the “Factor Analysis: Rotation” dialogue box.

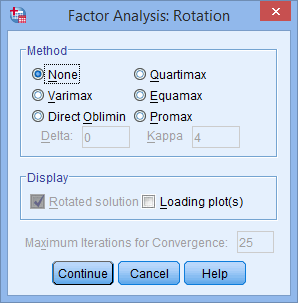
In the “Method” area, select the “Varimax” option. This will activate the “Rotated solution” option, which should be checked by default. Also, choose “Loading plot(s)” in the “Display” area.

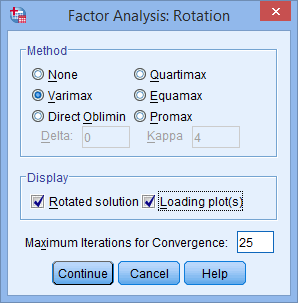
Keep in mind that you can explore alternative rotation options, such as Direct Oblimin, if needed, to achieve “simple structure” as discussed in further details.

Click “Continue” to return to the Factor Analysis dialogue box.

Click on the “Scores” button to access the “Factor Analysis: Factor Scores” dialogue box.

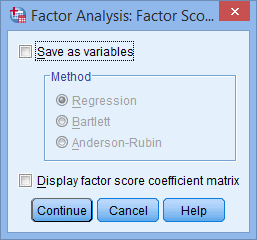
Check the “Save as variables” option and keep the “Regression” option selected.

Click “Continue” to return to the Factor Analysis dialogue box.

Click on the “Options” button to open the “Factor Analysis: Options” dialogue box.

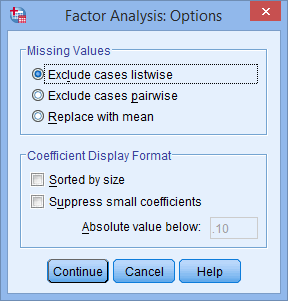
Here, check the options for “Sorted by size” and “Suppress small coefficients.” Additionally, change the value below “Absolute value” from “.10” to “.3”.

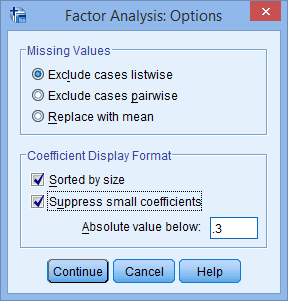
Click “Continue” to return to the Factor Analysis dialogue box.

Now, you have set all the necessary options for the PCA analysis. Click on the “OK” button to generate the output and proceed with the analysis. The results will be displayed based on the chosen settings and options.

Please follow these steps carefully to conduct a successful PCA analysis using SPSS Statistics.

Interpreting Principal Components Analysis (PCA) Output in SPSS

The output generated by SPSS Statistics after conducting PCA provides valuable insights into your analysis.

However, the process may require multiple iterations before arriving at a final solution. Here, we outline seven steps to interpret your PCA results and perform additional analysis in SPSS Statistics if necessary.

Step #1: Begin by interpreting the results of your assumption tests to ensure the validity of PCA on your data. Analyze scatterplots to check for linearity of variables (Assumption #2), assess sampling adequacy using the KMO Measure (Assumption #3), examine data suitability for reduction via Bartlett’s test (Assumption #4), and check for significant outliers in component scores (Assumption #5).

Look at the KMO value, aiming for a value of at least 0.6, with higher values indicating better suitability for PCA. Examine the significance (p-value) in the Bartlett’s Test row. If the p-value is less than 0.05, it suggests that the variables have significant correlations and PCA is appropriate. If the p-value is greater than 0.05, PCA may not be suitable.

Step #2: Inspect the initial extraction of components, where the number of components equals the number of variables. Focus on Initial Eigenvalues to grasp the major components extracted and the variance explained by each component.

Focus on the Initial Eigenvalues column. Interpret only factors with eigenvalues greater than 1.0. These represent significant components that explain substantial variance within the construct. Observe the % of Variance column, which shows how much variance each factor accounts for in the construct. The Cumulative % column displays the total variance accounted for by factors with eigenvalues above 1.0.

Step #3: Determine the number of ‘meaningful’ components you want to retain. You can use various methods, such as eigenvalue-one criterion, proportion of total variance accounted for, scree plot test, or interpretability criterion. Consider the implications of each option and how the selected rotation type (Varimax, Direct Oblimin, etc.) affects component loadings onto variables. Aim for a ‘simple structure’ with clear divisions of variables onto separate components.

Step #4: If you opt to retain a different number of components from the initial presentation by SPSS Statistics (Step #3), conduct Forced Factor Extraction. In this step, instruct SPSS Statistics to retain the specific number of components you arrived at earlier, and reanalyze your data accordingly.

Pattern Matrix Table: This table contains the extracted and rotated factors. Researchers can identify which survey items “load” on each factor, indicating their association with underlying components of the construct.

Step #5: Interpret the final, rotated solution by analyzing the revised Total Variance Explained output and the Rotated Components Matrix provided by SPSS Statistics.

Step #6: Report your results, including the criteria used for component extraction, the type of rotation employed, and other relevant decisions made during the analysis. In PCA, subjectivity plays a significant role, so transparent reporting of choices is crucial to understand potential variations in results.

Step #7: Lastly, assign scores to each component for each participant. For instance, based on our example, you might want a ‘motivation’ score derived from questions strongly loaded on Component 1. These scores can be useful for further analyses, like multiple regression. Two common methods for obtaining component scores are component scores and component-based scores.

Based on this analysis, researchers can make decisions about retaining or discarding survey items, leading to a finalized survey instrument for further testing and validation within a new sample.

when should you use the Principal Component Method of Factor Analysis?

1. If you want to reduce the number of dimensions in factor analysis but struggle to decide on the variables, PCA can be of great help.
2. When categorizing dependent and independent variables in your data, PCA becomes a valuable consideration.
3. If you seek to eliminate noise components in dimension analysis, PCA offers the most suitable computation method.

Other articles

Please read through some of our other articles with examples and explanations if you’d like to learn more about research methodology.