Effect Size (Examples) and Why Does It Matter?

Rate this post

Explore the significance of effect size with practical examples. Uncover its importance in research for a deeper understanding of statistical outcomes.

The significance of the relationship between variables or the difference between groups is indicated by the effect size. It shows how important a research finding is in practical applications.

A large effect size suggests that research findings have practical significance, whereas a small effect size suggests limited practical applications.

Please be aware that there are various methods for reporting results, and this article follows to the guidelines set forth by the American Psychological Association (APA).

Effect Size

A quantitative measure of the size of the experimental effect is called effect size. The stronger the relationship between two variables, the larger the effect size.

When comparing any two groups, you may determine how significantly different they are by looking at the effect size.

Research studies usually consist of two groups: a control group and an experimental group. An intervention or treatment that is meant to have an impact on a particular result could be the experimental group.

Example of Effect Size

For example, we might be interested in the effect of eating habits on the treatment of blood pressure. Whether the therapy has had a small, medium, or large effect on blood pressure will be shown by the effect size value.

Why does effect size matter?

Practical significance indicates that an effect is significant enough to have real-world implications, whereas statistical significance only indicates the existence of an effect in a study. P values indicate statistical significance, while effect sizes indicate practical significance.

Because statistical significance depends on sample size, it might be misleading when used alone. It is always more probable to find a statistically significant effect when the sample size is larger, regardless of how small the effect is in reality.

On the other hand, effect sizes don’t depend on sample size. Effect sizes are calculated solely by the data.

For this reason, effect sizes must be reported in research articles in order to demonstrate the findings’ practical significance.

Wherever possible, effect sizes and confidence intervals must be reported in accordance with APA guidelines.

Example:

A comprehensive study involving 13,000 participants in each of the control and experimental intervention groups compared two weight loss methods. The control group employed established, scientifically supported weight loss techniques, while the experimental group utilized a novel app-based approach.

Upon analyzing the results after six months, it was found that the mean weight loss (in kilograms) for the experimental intervention group (M = 10.6, SD = 6.7) was slightly higher than that of the control intervention group (M = 10.5, SD = 6.8). The observed difference was statistically significant (p = .01). However, the mere 0.1-kilogram difference between the groups may be considered negligible, and it doesn’t offer substantial insight into favoring one method over the other.

Including a measure of practical significance would illustrate how promising this new intervention is in compared to existing interventions.

When should you calculate the effect size?

There are numerous methods for calculating effect sizes. The two most widely used effect sizes are Pearson’s r and Cohen’s d. Whereas Pearson’s r indicates the strength of the association between two variables, Cohen’s d measures the size of the difference between two groups.

Cohen’s d

An appropriate effect size for comparing two means is Cohen’s d. It can be used, for instance, in conjunction with the reporting of results from ANOVA and the t-test. It’s also useful in meta-analysis.

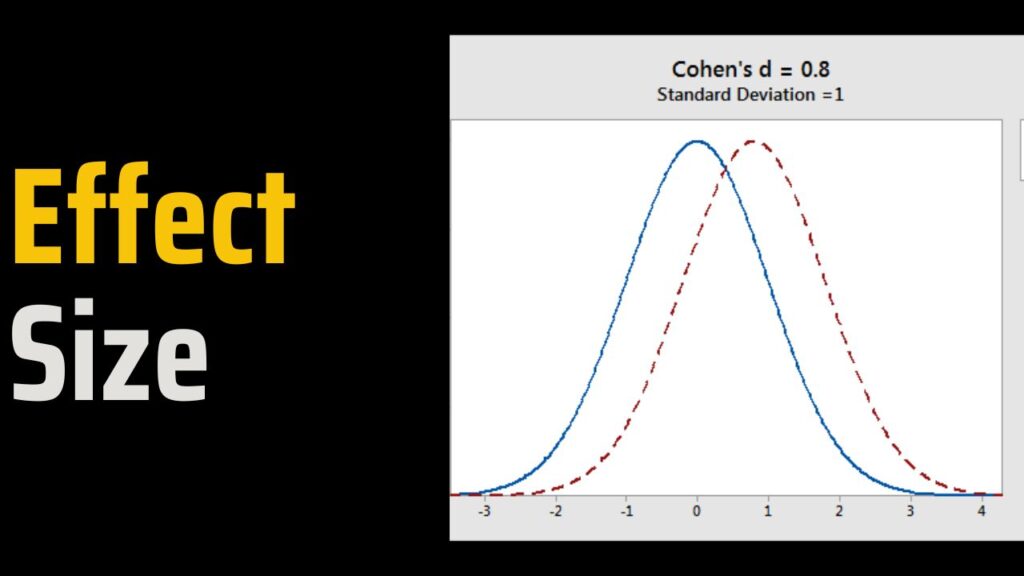
Cohen’s d is intended for comparing two groups. It calculates the standard deviation in units of difference between two means. It indicates how many standard deviations lie between the two means.

d = \frac {{\bar{x}_1} - {\bar{x}_2}}{s}

Cohen’s d formula	Explanation
$d = \frac {{\bar{x}_1} - {\bar{x}_2}}{s}$	$\bar{x}_1$ = mean of Group 1 $\bar{x}_2$ = mean of Group 2 s = standard deviation

Your research design will determine the standard deviation you use in the equation. You may use:

Pooled Standard Deviation: A pooled standard deviation derived from the data from both groups.

Standard Deviation from a Control Group: If your design contains a control and an experimental group, the standard deviation from the control group.
Standard Deviation from Pretest Data: If your repeated measures design comprises a pretest and posttest, the standard deviation from the pretest data.

Cohen proposed that an effect size of d = 0.2 is regarded as “small,” an effect size of 0.5 as “medium,” and an effect size of 0.8 as “large.” This indicates that even if a difference is statistically significant, it is insignificant if it is less than 0.2 standard deviations between the means of the two groups.

Example: Cohen’s d

In the calculation of Cohen’s d for the weight loss study, one computes the means of both groups and employs the standard deviation of the control intervention group:

\begin{align*} d = \frac {{\bar{x}_1} - {\bar{x}_2}}{s} \end{align*}

\begin{align*} d &= \dfrac{(10.6-10.5)}{6.8} \\ &=0.015 \end{align*}

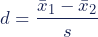
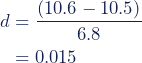
With a Cohen’s d of 0.015, the finding that the experimental intervention was more successful than the control intervention has little to no practical significance.

Pearson’s r Correlation

The degree of a linear relationship between two variables is expressed as Pearson’s r, or the correlation coefficient.

The bivariate relationship’s strength is expressed by the effect size parameter. The Pearson correlation effect size value ranges from -1, which represents a perfect negative correlation, to +1, which represents a perfect positive correlation.

Cohen (1988, 1992) states that the effect size is large if it changes more than 0.5, medium if it varies around 0.3, and low if it varies around 0.1.

To accurately calculate Pearson’s r from the raw data, it is best to use statistical software because the formula is quite complex.

r = \frac{ n\sum{xy}-(\sum{x})(\sum{y})}{% \sqrt{[n\sum{x^2}-(\sum{x})^2][n\sum{y^2}-(\sum{y})^2]}}

Pearson’s r formula	Explanation
$r = \frac{ n\sum{xy}-(\sum{x})(\sum{y})}{% \sqrt{[n\sum{x^2}-(\sum{x})^2][n\sum{y^2}-(\sum{y})^2]}}$	r_xy= strength of the correlation between variables x and y n = sample size ∑ = sum of what follows X = every x-variable value Y = every y-variable value XY = the product of each x-variable score times the corresponding y-variable score

The formula’s basic idea is to calculate how much of one variable’s variability is determined by the variability of the other variable.

Unit-free, Pearson’s r is a standardized scale for measuring correlations between variables. You can instantly compare the strengths of all correlations with one another.

One restriction is that Pearson’s r can only be used to interval or ratio variables, just like Cohen’s d. For ordinal or nominal variables, alternative measures of effect size must be used.

How can you determine whether an effect size is large or small?

According to Cohen’s criteria, effect sizes can be classified as small, medium, or large.

Cohen’s criteria for small, medium, and large effects varied depending on the measurement of effect size used.

Effect size	Cohen’s d	Pearson’s r
Small	0.2	.1 to .3 or -.1 to -.3
Medium	0.5	.3 to .5 or -.3 to -.5
Large	0.8 or greater	.5 or greater or -.5 or less

Cohen’s d ranges from 0 to infinity, while Pearson’s r falls between -1 and 1.

In general, a higher Cohen’s d indicates a larger effect size, whereas for Pearson’s r, values closer to 0 suggest a smaller effect size, and those nearer to -1 or 1 signify a more significant effect.

Furthermore, Pearson’s r provides information about the direction of the relationship:

A positive value (e.g., 0.7) means both variables increase or decrease together.

A negative value (e.g., -0.7) implies that one variable increases as the other decreases, or vice versa.

The criteria for a small or large effect size may also be influenced by what is typically found in research in your specific field, so be sure to check out other papers when interpreting effect size.

When should effect size be calculated?

Calculating effect sizes is useful before you begin your study and after you complete collecting data for your study.

Before you begin the study

Knowing the expected effect size allows you to calculate the minimal sample size required for statistical power to detect an effect of that size.

The possibility that a hypothesis test will identify a true effect, if any, is referred to as power in statistics. A false negative (a Type II error) is more likely to be rejected by a statistically powerful test.

Even when a result has practical significance, you might not be able to identify it as statistically significant if you don’t have enough power in your study. In such instance, despite the fact that there is an effect, you do not reject the null hypothesis.

You can use a set effect size and significance level to do a power analysis and find the sample size required at a certain power level.

Once you’ve completed your study

After gathering your data, you may calculate and report the actual affect sizes in your paper’s results and abstract sections.

Because they are easily compared and standardized, effect sizes are the raw data used in meta-analysis studies. To determine the average effect size of a certain finding, a meta-analysis can combine the effect sizes of numerous related studies.

However, meta-analysis studies can go a step further and explain why effect sizes may vary among studies examining a single topic. This could open up new ideas for research.

Why is it necessary to report effect sizes?

The p -value is not enough

Sometimes, a lower p-value indicates a stronger relationship between the two variables. Less than 5% is statistically significant, which indicates that the null hypothesis is unlikely to be true.

As a result, whereas an effect size indicates the extent to which an intervention works, a high p-value indicates its effectiveness.

Since the effect size is independent of sample size, unlike significance tests, it can be claimed that emphasizing the effect size encourages a more scientific approach.

To compare the results from studies conducted in different settings

Effect sizes, as opposed to p-values, can be used to compare study results quantitatively across different settings. In meta-analyses, it is commonly employed.