In this article you will learn the difference between parametric and non-parametric tes .
Statistical tests are employed in order to draw conclusions about the population from the sample. A statistical test is a formal method for determining if a hypothesis is acceptable that depends on the probability distribution. These hypothetical tests for differences are under the categories of parametric and nonparametric tests. The parametric test is a statistical test that provides data on the population parameter.
The nonparametric test, on the other hand, is one in which the researcher is unsure of the population parameter. Thus, give this article a thorough read to learn about the main differences between parametric and nonparametric tests.
Parametric Test
The hypothesis test that offers generalizations for claiming anything about the mean of the parent population is the parametric test. In this case, an often used t-test is one that is based on Student’s t-statistic.
The t-statistic is based on the presumption that the variables have a normal distribution and that the mean is either known or presumed to be known. For the sample, the population variance is calculated. The population’s relevant variables are assumed to be measured on an interval scale.
Examples of Parametric Test
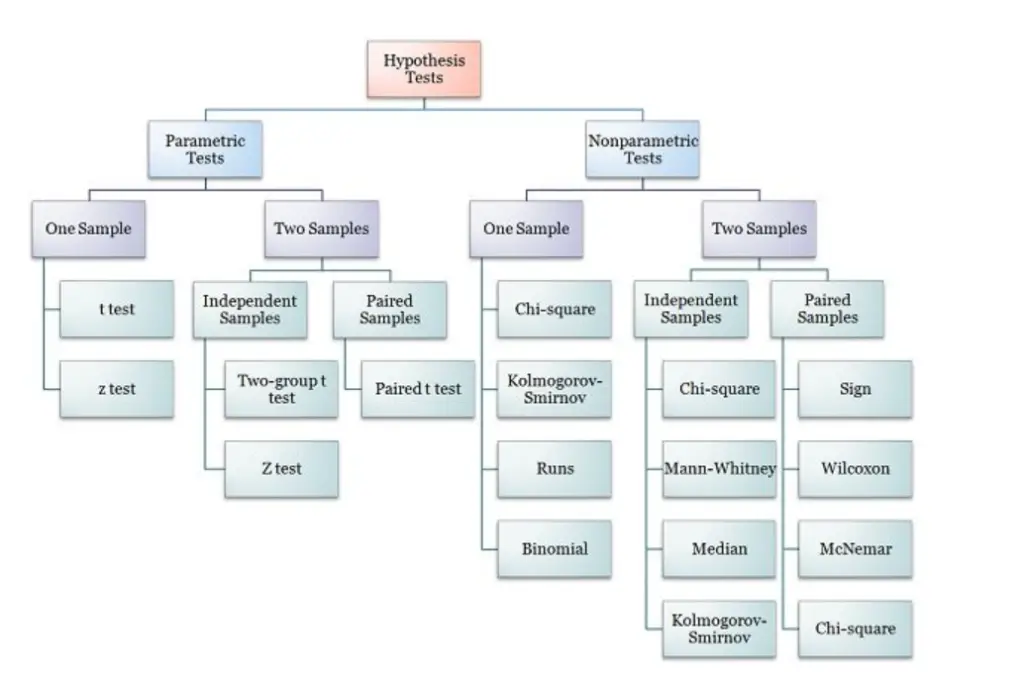
Some examples of parametric tests include the Independent Sample T Test, Paired samples T test, One way Analysis of Variance (ANOVA), One-way repeated measures Analysis of Variance
Non-parametric Test
The nonparametric test is defined as a hypothesis test that is not predicated on underlying assumptions, i.e., it is not dependent on the population’s distribution being represented by certain parameters.
The test mostly relies on differences in medians. Thus, it is also known as the distribution-free test. The test presupposes that the variables are measured on either a nominal or ordinal level. It is used if the independent variables are non-metric.
Non-parametric Test is w=used when
1-Sample is not normally distributed.
2- Sample size is small.
3- The variables are measured on nominal or ordinal scale
Examples of non-parametric tests
Some examples of nonparametric tests include the Mann-Whitney U Test, Wilcoxon Signed Rank Test, The Kruskal-Wallis Test, Friedman’s ANOVA
Difference between Parametric and Non-Parametric Test
| Parametric Test | Non-Parametric Test | |
| Definition | Statistical test that makes particular assumptions about the population parameter. | Statistical test applied to independent variables that are not metrics. |
| Central Tendency | Mean | Median |
| Correlation Test | Pearson | Spearman |
| Basis of test | Distribution | Arbitrary |
| Population | Known | Unknown |
| Measurement level | Interval or ratio | Nominal or ordinal |
| Applicability | Variables | Variables and Attributes |
| Tests | Independent Sample T Test, Paired samples T test, One way Analysis of Variance (ANOVA), One-way repeated measures Analysis of Variance | Mann-Whitney U Test, Wilcoxon Signed Rank Test, The Kruskal-Wallis Test, Friedman’s ANOVA |
1- Parametric Test, is the statistical test that makes particular assumptions about the population parameter. Whereas non-Parametric Test is the statistical test applied to independent variables that are not metrics.
2- In general, the mean is used to measure central tendency in parametric tests, while the median is used in nonparametric tests.
3- The parametric test uses Pearson’s coefficient of correlation to assess the strength of the relationship between two quantitative variables, whereas the nonparametric test uses Spearman’s rank correlation.
4- The test statistic in a parametric test is based on a distribution. Yet, in the case of a nonparametric test, the test statistic is arbitrary.
5- The population is clearly stated in the parametric test. In contrast, there is no information about the population in the nonparametric test.
6- While nonparametric tests are applicable to both variables and attributes, parametric tests only apply to variables.
7- The parametric test makes the assumption that the measurement of the variables is carried out at the interval or ratio level. As contrast to the nonparametric test, which uses nominal or ordinal scales to measure the relevant variable.
Hypothesis Tests Hierarchy
Advantages of parametric tests
For many datasets, parametric tests are helpful in analysing non-normal appropriations.
When the mean value serves as your central value and the size of your data set is comparatively large, a parametric test is used.
When provided quantitative and continuous data, this test is used.
This test is employed when the data has a normal distribution.
When the data is approximated on approximate ratio or interval scales of measurement, parametric tests are useful.
Advantages of non-parametric tests
When studied, nonparametric tests lead to less certain, more definite conclusions.
More robust and widely applicable.
Making strong and effective decisions is aided by this test.
If the median value is higher than the mean value, regardless of the size of the data set, a non-parametric test is taken into account.
In the case of solid mixing, these tests are performed to examine the sample findings.
When the data is approximated using various measurement scales, the tests are useful.
Less sensitive to outliers, which have a significant impact on the results of parametric tests.
Non-parametric tests are utilized when the population’s distribution is unknown,
If you’re learning about hypothesis testing, check out Hypothesis Testing book! You can find it at Amazon.
Frequently Asked Questions – FAQs
What is the benefit of parametric test?
A parametric test depends entirely on statistical data and has a higher likelihood of being accurate.
What is the benefit of nonparametric test?
Nonparametric tests are more robust and can be used in a wider variety of circumstances because they do not depend on any particular distribution.
What are the examples of non-parametric test?
Mann-Whitney U Test, Wilcoxon Signed Rank Test, The Kruskal-Wallis Test and Friedman’s ANOVA
What are the examples of parametric test?
Independent Sample T Test, Paired samples T test, One way Analysis of Variance (ANOVA) and One-way repeated measures Analysis of Variance
When to choose Parametric and Non-Parametric Tests?
A researcher undertaking statistical analysis finds it difficult to decide between the parametric and nonparametric test. While performing a hypothesis, a test is said to be parametric if the population’s characteristics are fully known through parameters. Nevertheless, if the population’s characteristics are unknown and a population test is required, the test is regarded to be nonparametric.
What central tendency value we consider for parametric and nonparametric test?
With a parametric test, the mean value is used, whereas for a non-parametric test, the median value is taken into account.
