Covariates are a fundamental concept in statistical analysis, particularly in the fields of research, experimental design, and data modeling. They play a crucial role in understanding and explaining variations in dependent variables.
In this blog post, we’ll explore what covariates are, their definition, and their various uses in statistical analysis.
Read More:
Statistical Analysis | 5 Steps & Examples
How To Calculate the Sample Size for Randomized Controlled Trials (RCT)
What is Primary Data Collection? Types, Advantages, and Disadvantages
How Do You Avoid Common Mistakes in Statistics?
How to build a PLS-SEM model using AMOS?
Understanding Standard Deviation: A Deep Dive into the Key Concepts
Traditionally, statisticians considered covariates to be a specific type of continuous predictor primarily used in ANOVA models, especially in the context of designed experiments (DOE). These experiments often involve categorical factors that researchers manipulate as primary variables of interest.
In such experimental designs, researchers typically control for most other potential explanatory variables (known as confounders) by carefully managing the experimental conditions and employing randomized designs. However, in some studies, analysts might recognize the presence of uncontrollable variables that could potentially influence the outcome. These uncontrollable variables are what covariates aim to address in the analysis.
What Are Covariates?
In statistics, a covariate, also known as a continuous independent variable or predictor, is a variable that is used to explain or predict variations in the dependent variable. The term “covariate” itself suggests a variable that covaries with another. In simpler terms, covariates are associated with or related to the variable you are trying to study or predict.
A covariate is a variable that is not the primary focus of an experiment but can have an impact on the dependent variable and the relationship between the independent variable and the dependent variable.
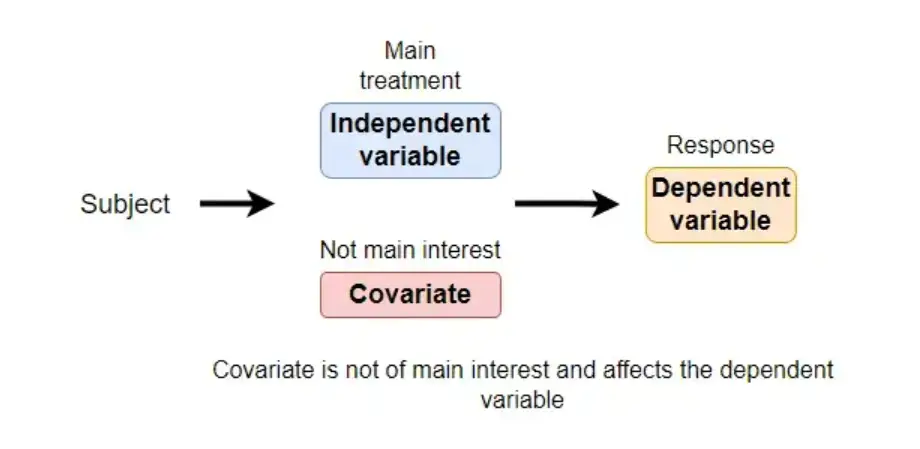
Covariates are not the main variables of interest in a study but are used to account for variations in the dependent variable, thus improving the precision of statistical models.
The covariate is not a planned variable, but it frequently appears in experiments as a result of the underlying experimental conditions.
To improve the statistical model’s accuracy and decrease its unexplained variation, covariates should be identified and examined. As a result, another name for the covariate is a control variable.
In statistics, a covariate can be thought of as an independent variable that complements or is associated with the dependent variable.
Essentially, any measurable variable that exhibits a statistical relationship with the dependent variable qualifies as a covariate. Consequently, a covariate is a potential explanatory or predictive variable for the dependent variable. It serves the purpose of helping to explain or predict variations in the dependent variable.
Read More:
A Glance At Derivatives & Formulas!
Principal Components Analysis (PCA) using SPSS
What is Multivariate Analysis?
Using Different Statistical Tools: A Guide to Choosing the Right Tool for Data Analysis
Type I vs Type II error in Hypothesis Testing
Example of Covariates
Let’s consider a practical example: a study examining the impact of a new teaching method on student performance.
In this case:
- The independent variable is the teaching method (e.g., traditional vs. innovative).
- The dependent variable is student performance (e.g., test scores).
- A covariate could be the students’ prior academic achievement, such as their grades in the previous semester.
Including the covariate (prior academic achievement) in the analysis allows researchers to control for variations in student performance that might be attributed to their prior academic history. This ensures that any differences in performance are more likely to be associated with the teaching method.
Example of a Covariate in an Experiment:
In an experiment aimed at examining the impact of the number of hours students study for a test on their educational achievement, the number of study hours serves as a covariate. It is considered a covariate because changes in the number of study hours correlate with changes in the students’ test scores.
Uses of Covariates
Covariates have several important uses in statistical analysis, research, and experimentation:
1. Control for Confounding Variables
Covariates are often used to control for the influence of extraneous or confounding variables. These are variables that are not the primary focus of the study but could affect the relationship between the independent and dependent variables. By including covariates in the analysis, researchers can statistically control for these confounding variables, ensuring that the observed effects are more accurately attributed to the independent variable of interest.
2. Enhance Model Precision
Covariates can improve the precision and accuracy of statistical models. By including relevant covariates, researchers can account for additional sources of variation in the dependent variable, reducing the error in the model. This, in turn, increases the reliability and predictive power of the model.
3. Address Heterogeneity
In research, it is common for participants or subjects to vary in characteristics that might influence the dependent variable. Covariates can help address this heterogeneity by accounting for individual differences and ensuring that the results are not driven by factors other than the independent variable.
4. Establish Causality
Covariates can help strengthen the argument for causal relationships in observational studies. By including covariates, researchers can address potential alternative explanations and establish more robust causal links between variables.
Use of Covariates in Research
Covariates play a critical role in research studies, particularly in cases where observational or experimental units exhibit heterogeneity.
In such studies, covariates act as the X variables in the statistical model, enhancing the precision of treatment effects. In observational study designs, covariates can be introduced to explore specific conditional effects, enhance predictive capabilities, and eliminate confounding variables that may affect the outcomes.
Covariates in research can be classified into two main types: independent variables and confounding variables.
- Independent variables are the variables directly under investigation in a study.
- Confounding variables are those covariates that are not initially considered by the researcher but can introduce bias into the results. Researchers can address and minimize the influence of confounding variables through careful study design, particularly by using randomization techniques. Randomizing the assignment of study participants helps distribute potential confounding variables evenly across comparison groups, reducing their impact on the study’s outcomes.
When to Include a Covariate
The decision to include a covariate in your experimental data analysis should be based on specific criteria:
- A Priori Specification: Covariates should be specified a priori, ideally in a pre-analysis plan. This means selecting covariates before conducting the experiment, helping prevent Type I error inflation (false positive conclusions), and retaining the power-enhancing benefits of covariates.
- Theoretical-Driven Selection: Your choice of covariates should be theoretically driven, guided by prior research on the subject you’re studying. This becomes especially crucial in nonexperimental designs where random assignment isn’t possible to mitigate covariate effects.
- Importance of Covariates: Identifying important covariates is essential to prevent misleading results and erroneous conclusions. However, including too many covariates can decrease the power of data analyses in detecting significant associations between predictor variables and the outcome variable.
Read More:
Difference between Descriptive and Inferential Statistics
Friedman Test: Example, and Assumptions
T-test | Example, Formula | When to Use a T-test
Chi-Square Test (Χ²) || Examples, Types, and Assumptions
Covariates and Analysis of Covariance (ANCOVA)
AN analysis of covariance (ANCOVA) is an extension of ANOVA that incorporates a covariate into the statistical model. It assesses the impact of the independent variable (the primary treatment variable) on the dependent variable while accounting for the presence of a covariate in the study.
In the example, a one-way ANOVA might have been used to examine the influence of plant genotypes on yield. However, without taking into account the impact of plant height (the covariate), the results could be misleading.
ANCOVA includes the covariate in the model and calculates genotype differences while adjusting for the effect of plant height. This approach enhances the model’s accuracy by accounting for the variance associated with the covariate.
In ANCOVA, the independent variables are categorical variables. For example, you might examine the effect of various depression treatments, where the independent variables represent the types of treatments individuals receive. Meanwhile, the dependent variable is typically a countable variable, such as scores on a self-scoring depression scale. However, within each treatment group, there is considerable unexplained variation. In this context, the covariate plays a crucial role:
Analysis of Variance (ANOVA) is a statistical test used to determine significant differences between categorical groups. In cases where covariates are absent, using Analysis of Covariance (ANCOVA) is necessary.
- Observed/Measured: Covariates are observed or measured variables, not manipulated by the researcher. They are characteristics inherent to the participants, and the researcher takes them into account during analysis.
- Control Variable: Covariates are control variables that serve to control or account for variations in the dependent variable. They help ensure that differences observed in the dependent variable are more likely to be related to the independent variables of interest.
- Continuous Variable: Covariates are continuous variables, often quantifiable characteristics that can vary across a range of values. For instance, in the case of depression treatment effectiveness, a covariate might be the initial level of depression, which can be measured on a continuous scale.
Advantages of ANCOVA
1. Ensuring Homogeneity of Regression
ANCOVA assumes that the association between the outcome variable and the covariate is consistent across the groups tested in the experiment.
2. Combining ANOVA and Regression
ANCOVA combines variance analysis and regression to control for covariate effects, enhancing the accuracy of the experiment.
3. Application in Different Research Designs
ANCOVA can be employed in experimental designs to control for non-randomizable interval-scale factors. It can also be used in observational designs to eliminate variables modifying the relationship between independent categories and interval-dependent variables.
4. Versatility
ANCOVA can be applied in non-experimental research when random assignment is infeasible, including non-random samples, surveys, and quasi-experiments.
5. One-Way and Two-Way ANCOVA
Depending on your research design, you can use one-way ANCOVA to determine significant differences among unrelated groups while statistically controlling for a confounding covariate. In a case involving two independent variables, a two-way ANCOVA is appropriate for examining significant two-way interaction effects and post hoc tests to delve deeper into the study results.
Read More:
A Useful Guide On Statistical Package For The Social Sciences [SPSS]
Differences Between Microsoft Excel and SPSS
Difference between Parametric and Non-Parametric Test
Difference Between One-tailed and Two-tailed Test
Conclusion
Covariates in statistical analysis help researchers control for confounding variables, enhance the precision of their models, address heterogeneity, and strengthen arguments for causality.
Understanding and appropriately using covariates is essential for robust and reliable research in various fields, including medicine, social sciences, and data analysis. The inclusion of covariates in statistical models is a valuable practice for anyone seeking accurate and meaningful results in their research.



