Using Different Statistical Tools: A Guide to Choosing the Right Tool for Data Analysis

In the realm of data analysis, statistical tools play a crucial role in uncovering valuable insights and making informed decisions.

The statistical methods used in conducting a study include planning, designing, collecting data, analysing, making relevant interpretations, and reporting research findings.

With the help of statistical analysis, previously meaningless data can be understood. If the right statistical tests are used, the results and inferences are accurate. This article aims to provide a comprehensive guide on different statistical tools and when to use them.

Descriptive Statistics

Descriptive statistics provides a summary of data, allowing analysts to gain insights into the distribution, central tendency, and variability of a dataset.

•Measures of Central Tendency

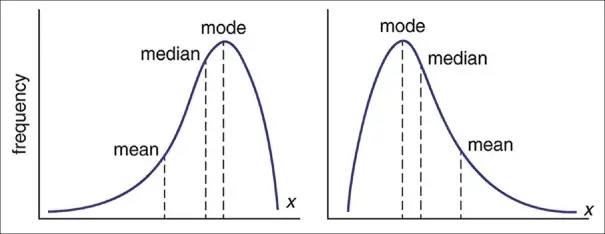
Measures of central tendency, such as mean, median, and mode, provide information about the central value or typical value of a dataset. The choice of measure depends on the nature of the data and the research question at hand.

Example of mean, variance, standard deviation

•Measures of Dispersion

Measures of dispersion, including range, variance, and standard deviation, describe the spread or variability of data points. These measures help in understanding how data points deviate from the central tendency.

•Measures of Skewness and Kurtosis

Skewness and kurtosis quantify the asymmetry and shape of a distribution, respectively. These measures provide insights into the departure from a normal distribution and help researchers identify potential outliers or peculiar patterns in their data.

It is a distribution with asymmetry of variables around its mean. The majority of the distribution is concentrated on the right of Figure in a negatively skewed distribution. The mass of the distribution is concentrated on the left of the figure in a positively skewed distribution, which causes the right tail to be longer.

Inferential Statistics

Inferential statistics involves making inferences or generalizations about a population based on a sample. It helps in drawing conclusions and testing hypotheses.

A hypothesis is proposed explanation for a phenomenon (plural: hypotheses). Thus, hypothesis tests are procedures for deciding logically whether observed effects are real or not.

Probability is a measure of the possibility that an event will occur. A number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty) is used to quantify probability.

The term “null hypothesis” (H0 “H-naught,” “H-null”) in inferential statistics means that there is no association (difference) between the population variables under study.

A statement between the variables is assumed to be true, which is denoted by the alternative hypothesis (H1 and Ha).

The P value (or computed probability) is the probability of the event occurring by chance if the null hypothesis is true. Researchers use the P value, a number between 0 and 1, to determine whether to reject or keep the null hypothesis.

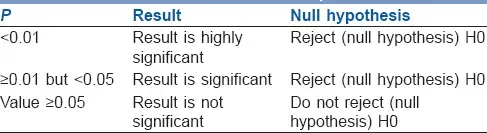
The null hypothesis (H0) is rejected if P value is less than the arbitrary value (also known as or the significance level). However, a Type I error occurs when the null hypothesis (H0) is incorrectly rejected.

•Hypothesis Testing

Hypothesis testing enables researchers to assess the statistical significance of relationships, differences, or effects observed in a sample. It involves setting up null and alternative hypotheses and using statistical tests to determine the likelihood of observing the results by chance.

•Regression Analysis

Regression analysis is used to examine the relationship between a dependent variable and one or more independent variables. It helps in understanding how changes in one variable relate to changes in another and enables prediction or estimation.

•Analysis of Variance (ANOVA)

ANOVA is a statistical technique used to compare means across multiple groups or treatments. It helps in determining if there are significant differences between the groups and identifies which group(s) differ from others.

Example of descriptive and inferential statistics

Time Series Analysis

Time series analysis focuses on analyzing data points collected over successive time intervals. It helps in understanding patterns, trends, and forecasting future values.

•Moving Averages

Moving averages smooth out fluctuations in data by calculating the average of a specific number of preceding data points. It aids in identifying trends and removing noise from the data.

•Exponential Smoothing

Exponential smoothing assigns different weights to past observations, giving more importance to recent values. It is useful for forecasting when there is a need to emphasize recent trends or patterns in the data.

•Autoregressive Integrated Moving Average (ARIMA)

ARIMA is a powerful time series model that incorporates autoregression, differencing, and moving average components. It can handle data with trends, seasonality, and irregular patterns, making it suitable for forecasting.

Multivariate Analysis

Multivariate analysis involves analyzing multiple variables simultaneously to uncover relationships, patterns, or dimensions within the data.

•Principal Component Analysis (PCA)

PCA is a dimensionality reduction technique that transforms a set of correlated variables into a smaller set of uncorrelated variables, known as principal components. It simplifies complex data and aids in visualizing and understanding the underlying structure.

•Factor Analysis

Factor analysis explores the interrelationships among a large number of variables by identifying latent factors. It helps in reducing data complexity, identifying underlying dimensions, and simplifying data interpretation.

•Cluster Analysis

Cluster analysis groups similar data points into clusters based on their characteristics or similarities. It is useful for segmentation, pattern recognition, and identifying subgroups within a dataset.

Choosing a parametric test: regression, comparison, or correlation

Flowchart: choosing a statistical test

You can select from a list of parametric tests using this flowchart.

When choosing a parametric test, you have several options, including regression, comparison, and correlation tests.

Here’s a brief overview of each type and when to use them:

1. Regression tests

Regression tests are used to analyze the relationship between variables and determine cause-and-effect relationships.

They estimate the effect of one or more independent variables on a dependent variable. If you have continuous variables and want to understand how changes in one variable affect another, regression tests are appropriate.

For example, you could use linear regression to examine how advertising expenditure impacts sales revenue.

	Predictor variable	Outcome variable	Research question example
Simple linear regression	•Continuous •1 predictor	•Continuous •1 outcome	What impact does income have on longevity?
Multiple linear regression	•Continuous •2 or more predictors	•Continuous •1 outcome	What impact do income and minutes of exercise per day on longevity?
Logistic regression	•Continuous	•Binary	What impact does medication have on the survival of a test subject?

Comparison tests

Comparison tests are designed to compare the means of different groups or conditions. They assess whether there are statistically significant differences in the outcome variable across categorical groups. If you want to compare means between two groups, you can use a t-test.

If you have more than two groups, analysis of variance (ANOVA) or its extension, multivariate analysis of variance (MANOVA), can be employed.

Comparison tests are useful when you want to determine if there are significant differences in outcomes based on categorical variables. For instance, you could use ANOVA to compare the mean scores of students from different educational backgrounds.

	Predictor variable	Outcome variable	Research question example
Paired t-test	•Categorical •1 predictor	•Quantitative •groups come from the same population	What impact do two different test preparation programs have on average exam scores for students in the same class?
Independent t-test	•Categorical •1 predictor	•Quantitative •groups come from different populations	What is the difference in average exam scores for students from two different schools?
ANOVA	•Categorical •1 or more predictor	•Quantitative •1 outcome	What is the difference in average pain levels among post-surgical patients given three different painkillers?
MANOVA	•Categorical •1 or more predictor	•Quantitative •2 or more outcome	What is the effect of flower species on petal length, petal width, and stem length?

Correlation tests

Correlation tests assess the strength and direction of the relationship between two continuous variables. They examine whether variables are related without implying a cause-and-effect relationship.

If you want to understand the degree of association between two quantitative variables, correlation tests are appropriate.

Pearson’s correlation coefficient is commonly used to measure the strength and direction of a linear relationship between variables.

For example, you might use correlation analysis to investigate the relationship between hours of study and exam performance.

	Variable	Research question example
Pearson’s r	2 continuous variables	How are hours of study and exam performance related?

Choosing a nonparametric test

When selecting a parametric test, consider the type of variables you have, the research question you want to address, and the assumptions of each test.

It’s important to ensure your data meets the assumptions of the chosen test, such as normality, linearity, and homoscedasticity. By choosing the appropriate parametric test, you can effectively analyze your data and draw meaningful conclusions.

	Predictor variable	Outcome variable	Use in place of
Spearman’s r	Quantitative	Quantitative	Pearson’s r
Chi square test of independence	Categorical	Categorical	Pearson’s r
Sign test	Categorical	Quantitative	One-sample t-test
Kruskal–Wallis H	Categorical 3 or more groups	Quantitative	ANOVA
ANOSIM	Categorical 3 or more groups	Quantitative 2 or more outcome variables	MANOVA
Wilcoxon Rank-Sum test	Categorical 2 groups	Quantitativegroups come from different populations	Independent t-test
Wilcoxon Signed-rank test	Categorical 2 groups	Quantitativegroups come from the same population	Paired t-test

When to perform a statistical test?

Statistical tests can be performed on data that has been obtained in a statistically valid manner – either through an experiment or from observations made using probability sampling methods.

Your sample size must be sufficient to roughly represent the true distribution of the population under study for a statistical test to be considered valid.

To choose the appropriate statistical test, you must be aware of:

• whether the assumptions made about your data are true.
• the kinds of variables you’re dealing.

Statistical assumptions

Statistical tests make certain common assumptions about the data they are testing:

Independence of observations (also known as no autocorrelation): The observations/variables in your test are not connected (for example, several measurements of a single test subject are not independent, whereas measurements of multiple different test subjects are independent).

Homogeneity of variance: the variance within each group being compared is similar across all groups. If one group has significantly greater variation than others, the test’s effectiveness will be limited.

Normality of data: Data that follows a normal distribution, often known as a bell curve, is said to be normal. The assumption only holds true for quantitative data.

You might be able to conduct a nonparametric statistical test, which enables comparisons without making any assumptions about the distribution of the data, if your data do not adhere to the assumptions of normality or homogeneity of variance.

You might be able to employ a test that takes into consideration the structure of your data (repeated-measures tests or tests with blocking variables) if your data is inconsistent to the assumption of independence of observations.

Other articles

Please read through some of our other articles with examples and explanations if you’d like to learn more about research methodology.