Randomized Controlled Trials (RCTs) are powerful tools in scientific research, providing a robust foundation for establishing causal relationships between interventions and outcomes. One critical aspect of designing an RCT is determining the appropriate sample size to ensure the study’s reliability and validity.
Calculating the sample size is a critical step in the design of randomized controlled trials (RCTs). The sample size is determined based on the primary outcome of the study and is crucial for ensuring the study’s statistical power and reliability.
This article provides an example of how to calculate sample size using simple formulas for an RCT comparing two groups of equal size.
Read More:
What is Randomized Controlled Trial?
Difference Between One-tailed and Two-tailed Test
Sample Size Formula for Continuous Outcome
The methods used to calculate sample size vary based on the kind of study design and the study’s outcome. In particular, the design of randomized controlled trials (RCTs) benefits greatly from these calculations. Generally, the primary result of the study is used to calculate the sample size.
The following provides an example of how to determine sample size for a randomized controlled trial (RCT) comparing two groups of similar size using the most basic formulas.
Assume the goal of the study was to examine the continuous outcome of a new hypertensive medication on systolic blood pressure (SBP), which is expressed in mmHg.
The sample size formula for a continuous outcome in an RCT with equal sample sizes in both groups is given by:

Where:
- n = the sample size in each of the groups
- μ1 = population mean in treatment Group 1
- μ2 = population mean in treatment Group 2
- μ1 − μ2 = the difference the investigator wishes to detect
- σ2 = population variance (SD)
- a = conventional multiplier for alpha* when alpha is 0.05
- b = conventional multiplier for power* when beta is 0.80
If the chosen significance level (α) is set at 0.05, the formula requires inputting the value 1.96 for a. Similarly, when selecting a beta (β) of 0.20, the formula necessitates using the value 0.842 for b.
Example to Calculate the Sample Size for Randomized Controlled Trials (RCT)
Let’s consider an example where researchers find a clinically relevant difference of 15 mmHg in systolic blood pressure (μ1 – μ2) between the treated and control groups.
They specify that this effect should be detectable with 80% power (0.80) at a significance level (α) of 0.05. Based on past similar experiments with comparable measuring methods and subjects, it is anticipated that the data will be approximately normally distributed with a standard deviation (SD) of 20 mmHg.
With these specifications, the formula can be applied, resulting in the determination that a sample size of 28 subjects per group is required to address the research question.

It’s important to note that these values (1.96 and 0.842) are referenced in a statistical table by researchers, and these table values are derived from the normal distribution of errors.
Example # 2
Let’s consider an outcome variable related to health, such as a disease or other health indicators. The focus is on evaluating the impact of a new treatment as compared to a traditional treatment on the prevalence of the outcome.
Hypothesis Formulation
The research question centers around whether the new treatment has any significant impact on the outcome. The hypothesis posits that after administering the new treatment, the prevalence of the outcome will decrease by 25 percentage points compared to traditional treatment.
Study Design
To test this hypothesis, we plan to conduct an experimental study using a randomized control trial (RCT) design. Participants will be randomly assigned to either a control group or one or more treatment groups.
Sample Size Calculation
The next step is to calculate the appropriate sample size for each group (n1 and n2) using Sambasiva’s formula, which is based on the formulated hypothesis.
Two-Sided Hypothesis Test
For a two-sided hypothesis test, where the alternative hypothesis is that there is a difference between the two groups, the formula is as follows:
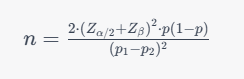
Here, p represents the pooled proportion of outcomes from both groups, p1 and p2 are the proportions from groups 1 and 2, and Zα/2 and Zβ are the corresponding Z-values for the chosen significance level and power, respectively.
Practical Calculation
Using an Excel sheet, we input the necessary information, including proportions, significance level, power, and Z-values. The calculated sample size for one group is approximately 70. Assuming equal sample sizes in both groups, the total sample size is 140. Considering a 20% addition for non-response or attrition, the final total sample size is 168.
One-Sided Hypothesis Test
For a one-sided hypothesis test, where the alternative hypothesis is that one proportion is less than or greater than the other, the formula is slightly modified:
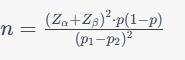
Here, Zα is the Z-value for the chosen significance level.
Practical Calculation
Inputting the necessary information, including the significance level and Z-value, we calculate a sample size of 131.
Conclusion:
Sample size calculation is a crucial step in the design of a randomized controlled trial. By following a systematic approach and utilizing appropriate formulas, researchers can ensure their study is adequately powered to detect meaningful effects.
This practical guide provides a clear roadmap for researchers embarking on RCTs and underscores the importance of meticulous planning in the research process.



